Donnerstag, 22. Januar 2015
Haben wir einen Statistiker an Bord?
mark793, 01:01h
Ich muss gestehen, ich habe es nicht so mit Statisik. Da befinde ich mich bekanntlich in guter Gesellschaft, denn Winston Churchill soll einmal gesagt haben, "es gibt Lügen, gottverdammte Lügen und Statistik". Ich bin versucht hinzuzufügen: Ach ja, und Bayessche Statistik. In einem Buch, das ich gerade lese, bin ich nämlich hierüber gestolpert:


Ich kann lesen, was da steht, ich kann mich auch auf den Kopf stellen und mit den Füßen wackeln, aber es will mir irgendwie nicht einleuchten, dass die Restwahrscheinlichkeit, wenn eines von drei Hütchen aufgedeckt ist, sich anders verteilen sollte als 50:50. Warum sollte, wenn die Kugel unter Hütchen A liegt, die Wahrscheinlichkeit, dass der Meister Hütchen B lüftet, 100 Prozent sein, wenn er doch auch C aufdecken könnte, wo ebenfalls keine Kugel ist? Was für A gilt, muss doch genauso für C gelten, und die Information, dass wir nach dem ersten Zug des Meisters wissen, unter Hütchen B war keine Kugel, ändert daran meines Erachtens gar nichts.
Aber wahrscheinlich müsste man es einfach lange genug auswürfeln.


Ich kann lesen, was da steht, ich kann mich auch auf den Kopf stellen und mit den Füßen wackeln, aber es will mir irgendwie nicht einleuchten, dass die Restwahrscheinlichkeit, wenn eines von drei Hütchen aufgedeckt ist, sich anders verteilen sollte als 50:50. Warum sollte, wenn die Kugel unter Hütchen A liegt, die Wahrscheinlichkeit, dass der Meister Hütchen B lüftet, 100 Prozent sein, wenn er doch auch C aufdecken könnte, wo ebenfalls keine Kugel ist? Was für A gilt, muss doch genauso für C gelten, und die Information, dass wir nach dem ersten Zug des Meisters wissen, unter Hütchen B war keine Kugel, ändert daran meines Erachtens gar nichts.
Aber wahrscheinlich müsste man es einfach lange genug auswürfeln.
... comment
mark793,
Donnerstag, 22. Januar 2015, 11:24
Per Mail
erreicht mich folgender Link (vielen Dank dafür nochmal von dieser Stelle). Spontan erscheint mir die dortige Darstellung des Ziegenproblems etwas einleuchtender, und ich muss mal gucken, ob und wie ich das mit dem Hütchenbeispiel im Buch in Übereinstimmung kriege. So wie ich das Ziegenbeispiel verstehe, ist der Wechsel weg von der ursprünglich gewählten Tür der entscheidende Move, um die Wahrscheinlichkeit zu eigenen Gunsten zu erhöhen. Demgegenüber habe ich das Beispiel im Buch eher so verstanden, dass für A eine a priori höhere Gewinn-Wahrscheinlichkeit spräche als für C, wenn der Meister das Hütchen B aufgedeckt hat, und der Wechsel empfehle sich nur, wenn der Spieler anfangs das Hütchen C ausgeguckt hätte.
Also heißt das, entweder habe ich das Hütchenbeispiel nicht richtig durchdrungen oder die Verfasserin hat es nicht verstanden, das Ziegenbeispiel so in eine andere Analogie zu kleiden, dass es immer noch einleuchtet.
Also heißt das, entweder habe ich das Hütchenbeispiel nicht richtig durchdrungen oder die Verfasserin hat es nicht verstanden, das Ziegenbeispiel so in eine andere Analogie zu kleiden, dass es immer noch einleuchtet.
... link
... comment
phom,
Donnerstag, 22. Januar 2015, 13:25
Es hilft vielleicht zum Verständnis, wenn man weiß, dass der Bayessche Ansatz durch eine andere Definition von Wahrscheinlichkeiten charakterisiert wird und eigentlich den traditionell frequentistischen Ansatz kritisiert. P(A) ist nach Bayes also gewissermaßen die mit Vorwissen gewichtete Plausibilität des Eintretens von A.
Die Wahrscheinlichkeit, bei einem fairen Würfel exakt eine bestimmte Ausprägung zu würfeln, beträgt grundsätzlich 1/6, das heißt, dass ich bei hundertmaligem Würfeln in Summe etwa 16 Mal die Eins würfeln werde, etwa 16 Mal die Zwei, ... Je größer die Zahl an Würfen, desto besser wird der Wert von 1/6 approximiert. Wenn ich nach einer größeren Zahl an Würfen immer wieder die Drei herausbekomme, dann würde gemäß dem traditionellen Ansatz die Wahrscheinlichkeit, eine weitere Drei zu würfeln, wiederum 1/6 sein. Bayes nutzt nun aber diese Information aus den vorherigen Würfen und verwendet sie für die Berechnung der Wahrscheinlichkeit der künftigen Würfe.
Dieser Ansatz ist nicht frei von Kritik, aber in bestimmten Fällen durchaus vielversprechend. Vielleicht noch ein Beispiel, das gut in die Dunkelkammer passt: Ich bin ein ziemlicher Pechvogel, was Fahrraddiebstähle anbelangt. An unserem früheren Wohnort wurde tatsächlich zwei Mal hintereinander mein Fahrrad entwendet. Nun könnte man sich, unter der Annahme, dass es hierzu verlässliche Daten gäbe, die Häufigkeit von Fahrraddiebstählen in diesem Stadtviertel ausrechnen, die möglicherweise ausgesprochen gering ist. Ich könnte also diesen offiziellen Wert modifizieren, indem ich meine scheinbar erhöhte Chance, bestohlen zu werden, berücksichtige. Wenn ich zwei Mal bestohlen wurde und der Nachbar drei Häuser weiter noch nie, dann sollte man nach Bayes die Wahrscheinlichkeit, dass ich auch noch ein drittes Mal bestohlen werde, höher ansetzen als die, dass mein Nachbar ein Mal bestohlen wird. Gewissermaßen ist dies der Versuch, Unsicherheit quantifizierbar zu machen.
Zurück zum Beispiel mit dem Magiermeister:
In der Ausgangssituation trägt die (Laplace-)Wahrscheinlichkeit, dass sich die Kugel unter einem Hütchen befindet:

Deckt man ein Hütchen auf, wodurch noch zwei verbleiben, in denen sich in einer die Kugel befinden muss, ergibt sich eine (Laplace-)Wahrscheinlichkeit von
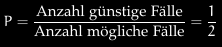
wie Sie richtig ausgeführt haben. Mit dem Bayesschen Ansatz sieht das nun etwas anders aus. Sie beruht auf Plausibilitätsannahmen. Es ist plausibel, dass der Meister das Spiel nicht vorzeitig beenden möchte, insofern hat er mit der ursprünglichen Entscheidung, B (und nicht A) aufzudecken, eine relevante Information mitgeliefert. Mit dem Bayes-Theorem (das man herleiten könnte) sieht das wie folgt aus:
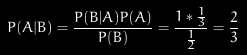
Wobei P(A) die Priori-Wahrscheinlichkeit ist (bevor der Magier das B-Hütchen aufdeckt), P(A|B) kann man demnach als Posteriori-Wahrscheinlichkeit bezeichnen.
Hier ist auch noch ein gutes Beispiel.
Die Wahrscheinlichkeit, bei einem fairen Würfel exakt eine bestimmte Ausprägung zu würfeln, beträgt grundsätzlich 1/6, das heißt, dass ich bei hundertmaligem Würfeln in Summe etwa 16 Mal die Eins würfeln werde, etwa 16 Mal die Zwei, ... Je größer die Zahl an Würfen, desto besser wird der Wert von 1/6 approximiert. Wenn ich nach einer größeren Zahl an Würfen immer wieder die Drei herausbekomme, dann würde gemäß dem traditionellen Ansatz die Wahrscheinlichkeit, eine weitere Drei zu würfeln, wiederum 1/6 sein. Bayes nutzt nun aber diese Information aus den vorherigen Würfen und verwendet sie für die Berechnung der Wahrscheinlichkeit der künftigen Würfe.
Dieser Ansatz ist nicht frei von Kritik, aber in bestimmten Fällen durchaus vielversprechend. Vielleicht noch ein Beispiel, das gut in die Dunkelkammer passt: Ich bin ein ziemlicher Pechvogel, was Fahrraddiebstähle anbelangt. An unserem früheren Wohnort wurde tatsächlich zwei Mal hintereinander mein Fahrrad entwendet. Nun könnte man sich, unter der Annahme, dass es hierzu verlässliche Daten gäbe, die Häufigkeit von Fahrraddiebstählen in diesem Stadtviertel ausrechnen, die möglicherweise ausgesprochen gering ist. Ich könnte also diesen offiziellen Wert modifizieren, indem ich meine scheinbar erhöhte Chance, bestohlen zu werden, berücksichtige. Wenn ich zwei Mal bestohlen wurde und der Nachbar drei Häuser weiter noch nie, dann sollte man nach Bayes die Wahrscheinlichkeit, dass ich auch noch ein drittes Mal bestohlen werde, höher ansetzen als die, dass mein Nachbar ein Mal bestohlen wird. Gewissermaßen ist dies der Versuch, Unsicherheit quantifizierbar zu machen.
Zurück zum Beispiel mit dem Magiermeister:
In der Ausgangssituation trägt die (Laplace-)Wahrscheinlichkeit, dass sich die Kugel unter einem Hütchen befindet:

Deckt man ein Hütchen auf, wodurch noch zwei verbleiben, in denen sich in einer die Kugel befinden muss, ergibt sich eine (Laplace-)Wahrscheinlichkeit von
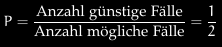
wie Sie richtig ausgeführt haben. Mit dem Bayesschen Ansatz sieht das nun etwas anders aus. Sie beruht auf Plausibilitätsannahmen. Es ist plausibel, dass der Meister das Spiel nicht vorzeitig beenden möchte, insofern hat er mit der ursprünglichen Entscheidung, B (und nicht A) aufzudecken, eine relevante Information mitgeliefert. Mit dem Bayes-Theorem (das man herleiten könnte) sieht das wie folgt aus:
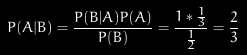
Wobei P(A) die Priori-Wahrscheinlichkeit ist (bevor der Magier das B-Hütchen aufdeckt), P(A|B) kann man demnach als Posteriori-Wahrscheinlichkeit bezeichnen.
Hier ist auch noch ein gutes Beispiel.
... link
mark793,
Donnerstag, 22. Januar 2015, 14:28
Ihr Beispiel mit dem Fahrrad leuchtet mir völlig ein, wobei ich allerdings dazu neigen würde, das Risiko nicht unbedingt am Besitzer an sich festzumachen, sondern vielleicht auch in Betracht zu ziehen, dass Sie beim Fahrraderwerb ein besseres Händchen hatten, Räder auszuwählen, die für Diebe interessanter sind als die Möhre des Nachbarn. Oder dass Sie dazu neigen, bei der Anschaffung eines Fahrradschlosses zu sehr auf Billigware zu setzen. ;-)
Grundsätzlich stehe ich dem Versuch von Bayes, vorhandenes Vorwissen in der Wahrscheinlichkeitsberechnung einzupreisen, aufgeschlossen gegenüber. Aller Erfahrung nach wird es nämlich eher nicht passieren, dass Affen beim wilden Rumtippen auf Tastaturen zufällig Goethes "Faust" reproduzieren, auch wenn man diese Möglichkeit natürlich von vornherein nicht ausschließen kann. Genausowenig rechne ich ernsthaft damit, dass die Stehlampe hier im Arbeitszimmer plötzlich umfällt, weil sie zufälligerweise grade mal nur auf einer Seite von Luftmolekülen im Rahmen der Brwonschen Molekularbewegung angeditscht wurde. Aber passieren kann das freilich schon.
Mein Problem mit der Erklärung des Hütchenspiels ist nach wie vor, dass sie sich darauf kapriziert, die Wahl des Meisters von B gehe voll zu Lasten von A. Ich aber meine, die Wahl von B ist genausosehr auch eine Entscheidung gegen das Hütchen C, also warum soll das eine weniger relvante Information sein als dass A beim ersten Zug nicht geöffnet wurde? Ich kriege das in der Form immer noch nicht zusammen mit dem Ziegentheorem, bei dem mir im Prinzip einleuchtet, dass der Wechsel von der zunächst angedachten Tür zur anderen verbleibenden Tür die Gewinnchance erhöht. Das Hütchenbeispiel lese ich aber so, als komme de, Hütchen A allein dadurch, dass der Meister zunächst B aufdeckte, eine höhere Gewinnchance zu. Und da hakt es bei mir immer noch.
Grundsätzlich stehe ich dem Versuch von Bayes, vorhandenes Vorwissen in der Wahrscheinlichkeitsberechnung einzupreisen, aufgeschlossen gegenüber. Aller Erfahrung nach wird es nämlich eher nicht passieren, dass Affen beim wilden Rumtippen auf Tastaturen zufällig Goethes "Faust" reproduzieren, auch wenn man diese Möglichkeit natürlich von vornherein nicht ausschließen kann. Genausowenig rechne ich ernsthaft damit, dass die Stehlampe hier im Arbeitszimmer plötzlich umfällt, weil sie zufälligerweise grade mal nur auf einer Seite von Luftmolekülen im Rahmen der Brwonschen Molekularbewegung angeditscht wurde. Aber passieren kann das freilich schon.
Mein Problem mit der Erklärung des Hütchenspiels ist nach wie vor, dass sie sich darauf kapriziert, die Wahl des Meisters von B gehe voll zu Lasten von A. Ich aber meine, die Wahl von B ist genausosehr auch eine Entscheidung gegen das Hütchen C, also warum soll das eine weniger relvante Information sein als dass A beim ersten Zug nicht geöffnet wurde? Ich kriege das in der Form immer noch nicht zusammen mit dem Ziegentheorem, bei dem mir im Prinzip einleuchtet, dass der Wechsel von der zunächst angedachten Tür zur anderen verbleibenden Tür die Gewinnchance erhöht. Das Hütchenbeispiel lese ich aber so, als komme de, Hütchen A allein dadurch, dass der Meister zunächst B aufdeckte, eine höhere Gewinnchance zu. Und da hakt es bei mir immer noch.
... link
rocky raccoon,
Donnerstag, 22. Januar 2015, 15:57
Bei mir hakt es analog zu Hr. Mark. Zuerst habe eine Gewinnchance von 1/3. Nach Aufdeckung des einen (falschen) Hütchens habe ich eine Chance von 1/2. Egal, ob ich wechsle oder nicht.
Das ist aber eine Mindermeinung, wie man nachgoogeln kann.
Das ist aber eine Mindermeinung, wie man nachgoogeln kann.
... link
mark793,
Donnerstag, 22. Januar 2015, 17:39
Auf alle Fälle ist die Lösung mit den ungleich verteilten Wahrscheinlichkeiten zwischen den beiden verbleibenden Hütchen kontraintuitiv, soviel ist sicher. Ansonsten stecken da halt auch ein paar Grundannahmen über das Spiel und das Verhalten des Moderators drin, die in dem obigen Buchauszug nicht klar benannt sind (näheres dazu hier).
... link
... comment
fallenbeck,
Donnerstag, 22. Januar 2015, 16:46
Ich habe das mal simuliert
Also, das stimmt. Und ich habe damals(tm) auch eine Weile gebraucht, bis ich mich damit abgefunden hatte. :-)
Ich habe gerade nochmal eine Simulation geschrieben und das 1 Mio mal laufen lassen mit folgendem Ergebnis:
Finished playing 1000000 games of each type
Successful games when initial choice was not changed: 332677 (33.27 %)
Successful games when changing the initial choice: 666607 (66.66 %)
Das Python-Script zur Simulation kannst Du Dir hier herunterladen und selbst nochmal mit herumspielen:
http://www.fallenbeck.com/pub/game.py
Ich habe gerade nochmal eine Simulation geschrieben und das 1 Mio mal laufen lassen mit folgendem Ergebnis:
Finished playing 1000000 games of each type
Successful games when initial choice was not changed: 332677 (33.27 %)
Successful games when changing the initial choice: 666607 (66.66 %)
Das Python-Script zur Simulation kannst Du Dir hier herunterladen und selbst nochmal mit herumspielen:
http://www.fallenbeck.com/pub/game.py
... link
mark793,
Donnerstag, 22. Januar 2015, 17:11
Ja sapperlot, das ist mal ein Ansatz, wie ich ihn liebe: die Affen wirklich an die Schreibmaschinen gesetzt und lesbaren Text inmitten all des Grundrauschens erzeugt! Das war es in etwa, was ich weiter oben damit meinte, man müsste es mal auswürfeln.
... link
... comment
kid37,
Donnerstag, 22. Januar 2015, 19:29
Gott würfelt doch
Wie häufig (statistisch gesehen) wissen Akte-X-Seher mehr. In Improbable nämlich lässt Burt Reynolds als Gott mit solchen Hütchenspielertricks die Wahrscheinlichkeiten durcheinanderfliegen. Dieser Bayes-Ansatz führt dann wohl dahin, daß es eben doch keine Wahrheit da draußen gibt, wie es übliche statistische Modelle suggerieren. (Das aber nur als Nebenbemerkung für die weitere Forschung.)
... link
mark793,
Donnerstag, 22. Januar 2015, 22:26
Quid est veritas? fragte bereits mein biblischer Lieblingsheld Pontius Pilatus, und wenngleich Bayes nicht im Geschäft der absoluten Wahrheiten tätig war, so definiert sein Wahrscheinlichkeitsbegriff zumindest den "Grad vernünftiger Erwartung", also als Maß für die Glaubwürdigkeit einer Aussage, der von 0 (falsch, unglaubwürdig) bis 1 (glaubwürdig, wahr) reicht.
Damit ist dieser Ansatz geradezu prädestiniert für die großen Fragen, mit denen sich unsere symphatischen FBI-Spezialagenten herumzuplagen haben: Gibt es Außerirdische - und wenn ja, wusste die US-Regierung davon? Das sind bedingte Wahrscheinlichkeiten der Form P(A\B). Eine etwas abstraktere und doch präzisere Art. I want to believe auszudrücken...
Damit ist dieser Ansatz geradezu prädestiniert für die großen Fragen, mit denen sich unsere symphatischen FBI-Spezialagenten herumzuplagen haben: Gibt es Außerirdische - und wenn ja, wusste die US-Regierung davon? Das sind bedingte Wahrscheinlichkeiten der Form P(A\B). Eine etwas abstraktere und doch präzisere Art. I want to believe auszudrücken...
... link
schlotte,
Freitag, 23. Januar 2015, 07:20
Gibts die Hütchenspieler in Malle noch?Die brauchen keinen Bayes,um es Euch zu erklären ^^
... link
crispinus,
Freitag, 23. Januar 2015, 10:18
Vor C kommt A im Alphabet, für mich die entscheidende Komponente. Der Hütchenspieler will "weg" von A, da es die mental erste Wahl ist, weshalb er den Mitspieler auf C bringen will, denn dieser soll den nächsten Schritt machen, also den nächsten Buchstaben wählen.
So sehe ich es (als nicht-Hütchenspieler) intuitiv, weil ich, wie der ähnlich alphabetisierte Gegner, eine unausgesprochene Präferenz für den ersten Buchstaben des Alphabets habe /unterstelle, genauso wie ich immer zuerst die Nummer 1 wähle . . . .
Das ist in meinen Augen die fehlende Prämisse in diesem Wahrscheinlichkeitsproblem.
Die Lösung bleibt gleich.
So sehe ich es (als nicht-Hütchenspieler) intuitiv, weil ich, wie der ähnlich alphabetisierte Gegner, eine unausgesprochene Präferenz für den ersten Buchstaben des Alphabets habe /unterstelle, genauso wie ich immer zuerst die Nummer 1 wähle . . . .
Das ist in meinen Augen die fehlende Prämisse in diesem Wahrscheinlichkeitsproblem.
Die Lösung bleibt gleich.
... link
mark793,
Freitag, 23. Januar 2015, 14:14
Ähnliche Überlegungen über die Motivationen des Moderators sind auch in dem Wikipedia-Artikel zum Ziegen-Theorem erwähnt, nur dass es da um die Nummerierung der Türen geht und nicht die Buchstaben der Hütchen.
Da müssten wir Niels mal fragen, ob er diesen Faktor in seiner Simulation auch berücksichtigt hat. Ich denke indes, wenn tatsächlich der Wechsel des Hütchens oder der Tür derjenige Faktor ist, welcher die Gewinnwahrscheinlichkeit signifikant erhöht, dann sollten alphanumerische Präferenzen eigentlich keine große Rolle spielen.
Da müssten wir Niels mal fragen, ob er diesen Faktor in seiner Simulation auch berücksichtigt hat. Ich denke indes, wenn tatsächlich der Wechsel des Hütchens oder der Tür derjenige Faktor ist, welcher die Gewinnwahrscheinlichkeit signifikant erhöht, dann sollten alphanumerische Präferenzen eigentlich keine große Rolle spielen.
... link
mark793,
Freitag, 23. Januar 2015, 17:35
Per Mail
kam grade noch dieser sehr kompakte Erklärungsansatz rein:
Es existieren Hütchen A, B, C - Gewinn liegt unter Hütchen A, Verlust
unter B und C.
Folgende Fälle treten auf, wenn der Spieler sich nicht umentscheidet
(Verhalten des Moderators ist völlig egal):
Spieler wählt A - gewinnt
Spieler wählt B - verliert
Spieler wählt C - verliert.
=> Gewinnchance 1/3
Folgende Fälle treten auf, wenn sich der Spieler umentscheidet:
Spieler wählt A, Moderator deckt B oder C auf, Spieler wählt C oder B -
verliert
Spieler wählt B, Moderator deckt C auf, Spieler wählt A - gewinnt
Spieler wählt C, Moderator deckt B auf, Spieler wählt A - gewinnt.
=> Gewinnchance 2/3
Es existieren Hütchen A, B, C - Gewinn liegt unter Hütchen A, Verlust
unter B und C.
Folgende Fälle treten auf, wenn der Spieler sich nicht umentscheidet
(Verhalten des Moderators ist völlig egal):
Spieler wählt A - gewinnt
Spieler wählt B - verliert
Spieler wählt C - verliert.
=> Gewinnchance 1/3
Folgende Fälle treten auf, wenn sich der Spieler umentscheidet:
Spieler wählt A, Moderator deckt B oder C auf, Spieler wählt C oder B -
verliert
Spieler wählt B, Moderator deckt C auf, Spieler wählt A - gewinnt
Spieler wählt C, Moderator deckt B auf, Spieler wählt A - gewinnt.
=> Gewinnchance 2/3
... link
... comment
